what does a base raised to a negative exponent mean
Many students already struggle to sympathise negative numbers, exponent rules and fractions. So what happens when you add negative exponents to the equation?
Total anarchy.
Well, not really. But understanding negative exponents is an important building cake for high school-level math courses, and information technology's also a concept many students detect challenging. When you gradually build on your students' knowledge, you'll ensure they're set to tackle challenging bug in and out of the classroom.
If you're not certain where to begin, this blog postal service volition assist you lot transform your unit of measurement on negative exponents into a positive experience for y'all and your students!
Negative exponents rules

Like everything else in math class, negative exponents have to follow rules. If y'all demand a reminder , here's a quick recap of the 7 rules of exponents:
- Product of powers: Add powers together when multiplying like bases
- Quotient of powers dominion: Decrease powers when dividing similar bases
- Power of powers dominion: Multiply powers together when raising a power by another exponent
- Ability of a product dominion: Distribute power to each base of operations when raising several variables by a power
- Ability of a quotient rule: Distribute power to each base when raising several variables by a ability
- Zero power rule: Any base raised to the ability of zilch becomes 1
- Negative exponent rule: To modify a negative exponent to a positive one, flip it into a reciprocal.
Remind students that the rules stay the same with negative exponents — there merely might be a few extra steps to follow.
A quick review of negative numbers
Negative numbers require a certain amount of abstract thinking that doesn't always come naturally. But without a solid agreement of negative numbers, students won't be set to tackle negative exponents.
Here'due south a quick review:
A negative number is whatever number less than cypher.
Negative numbers are expressed with a negative sign. For instance, -4 is four less than zero.
It'due south helpful to think of negative numbers as existing on a number line:
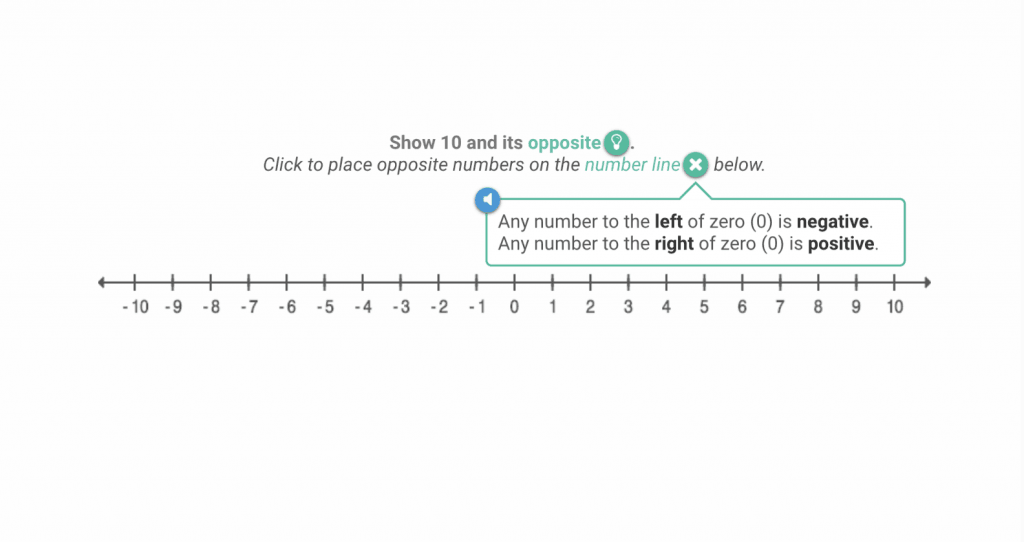
When you add and subtract negative numbers, you're either moving to the right or the left of the number line.
When you subtract a negative number you move to the left of the number line, because it's the same as adding a positive number. If you're calculation a negative number yous movement to the correct considering it'southward the same equally subtracting a positive number.
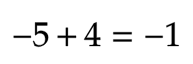
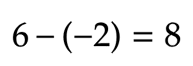
When you multiply a negative number by a positive number (or vice versa), the product volition be negative. If you multiply ii negative numbers or two positive numbers, the result volition be positive.
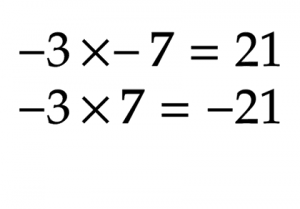
Multiplying different signs will ever give you a negative product, and multiplying the same signs will give you a positive product. Always assume the number is positive if there's no sign in front of it.
What do negative exponents hateful?
We already know that positive exponents are a way of expressing repeated multiplication. For case:
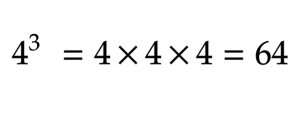
There are a few unlike ways of thinking nearly negative exponents, but in general, negative exponents are the opposite of positive ones.
All negative exponents can exist expressed as their positive reciprocal. A reciprocal is a fraction where the numerator and denominator switch places.
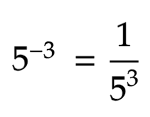
How tin something exist flipped into a reciprocal if it wasn't a fraction to start?
We know that numbers can be expressed in more than i way. For example, eight can also be written every bit:
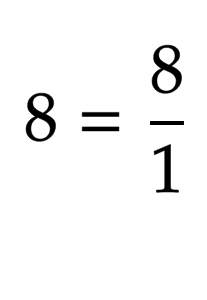
So, negative exponents can exist expressed as the positive reciprocal of the base of operations multiplied by itself x times.
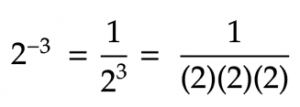
The larger the negative exponent, the smaller the number information technology represents. While positive exponents indicate repeated multiplication, negative exponents represent repeated sectionalization. That'south why 2-3is greater than 2-6.
How to solve negative exponents
Near questions will ask you to solve negative exponents by expressing them as positive equations. Hither's how:

Flip the base and exponent into the reciprocal, then solve the denominator. Divide the numerator by the denominator to find the final decimal.
Multiplying and dividing negative exponents
We've already covered multiplying exponents, but hither's a quick review on how to multiply and divide negative exponents.
Multiplying negative exponents
Good news! The rules for multiplying exponents are the aforementioned, even when the exponent is negative.
If the bases are the same, add the exponents. Remember to keep in mind the rules for adding and subtracting negative numbers.
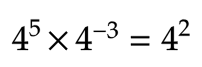
If the bases are different only the exponents are the same, multiply the bases and leave the exponents the way they are.
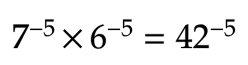
If in that location'south cipher in common, go directly to solving the equation. Flip the exponents into their reciprocals, and so multiply.
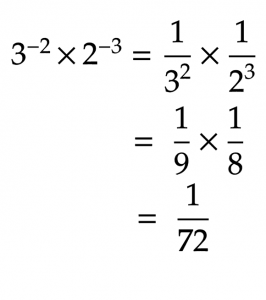
If you demand a reminder, check out our mail service on How to Multiply Fractions.
Dividing negative exponents
Dividing negative exponents is almost the aforementioned every bit multiplying them, except you're doing the opposite: subtracting where you would have added and dividing where you would have multiplied.
If the bases are the aforementioned, subtract the exponents.
Think to flip the exponent and make it positive, if needed.
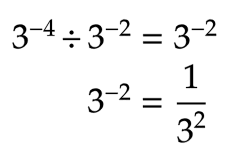
If the exponents are the same but the bases are different, divide the bases beginning.
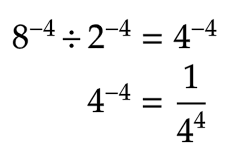
If there'due south zip in common, go straight to solving the equation.
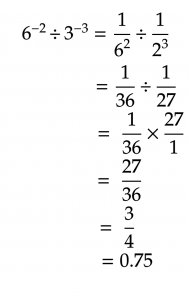
For a refresher on dividing fractions, check out our How to Divide Fractions blog post.
Negative numbers with exponents

What happens if the base is negative instead of the exponents?
If the exponent is positive, piece of work with it as you would a regular exponent, only remember ii things:
- If the base is negative and the exponent is an even number, the final product volition always bea positive number.
- If the base is negative and the exponent is an odd number, the final production will always bea negative number.
If in that location are parentheses effectually the negative base, the power applies to the entire equation -- including the negative sign. If there are no parentheses, the power applies merely to the base and not to the negative sign.
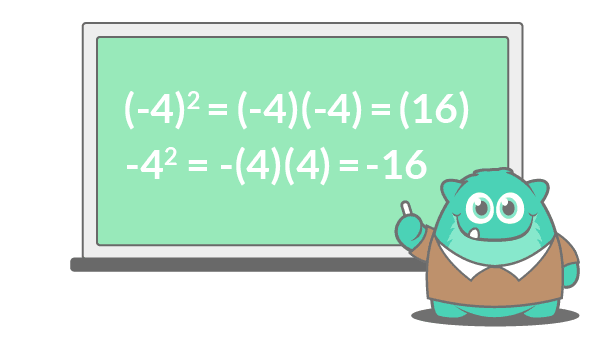
Since the commencement instance is beingness raised to an even power, the two negative signs cancel out and you're left with a positive product. If the exponent was an odd power, the product would be negative because there would be one number that couldn't abolish out.
In the 2nd instance, the positive power only applies to the four, non to the negative sign. In this example, the negative sign tells yous the product will be negative whether the power is odd or even.
Simplifying negative exponents
Multiplying, dividing and understanding negative exponents is the first footstep to simplifying expressions with negative exponents.
Remember: all the steps covered above hold truthful no matter how complicated the expression is.
Let'south start past multiplying negative exponents with variables.
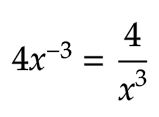
In this example, the power only applies to the x base, not the four. To brand information technology a positive expression, flip the ten to the reciprocal and go on the 4 on top.
Allow's try something a niggling more complicated.
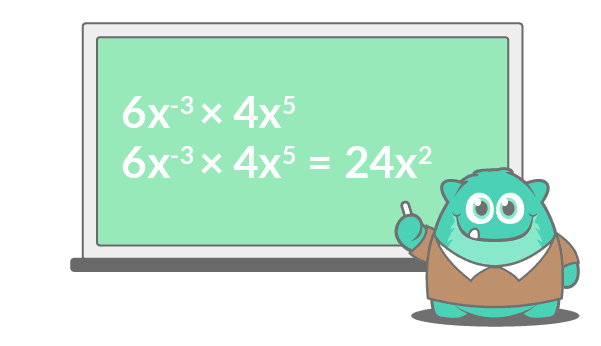
The variables hither are the same, so according to the first exponent rule, nosotros can multiply the numbers, keep the base the same and add together the exponents together.
Multiply the 6 and 4 for a product of 24. Then, add together the exponents together to multiply the x variables.
What about dividing negative exponents with variables?
Let's start with a simple example:
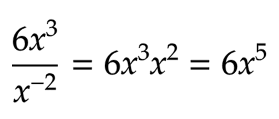
To make the negative exponent positive, move the ???? to the summit of the equation and multiply.
Here's an example of negative exponents with multiple variables:
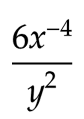
Since the negative exponent only applies to the variable, move 𝑥-4 to the bottom of the equation to make it positive, and leave the vi where information technology is.
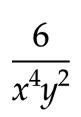
And at that place's your simplified equation!
Let'due south try some other one.

Kickoff, redistribute the ability to the inside of the brackets, following the third exponent rule.
Then, flip the 𝑥 variables with negative exponents to their reciprocal.
Finally, multiply the 𝑥 variables by adding the exponents together.
Let's practise one more.

To beginning, either foursquare the equation or move the parentheses first. We'll begin by squaring the acme subclass and redistributing the power.
Then, motility the negative exponents down or up, depending on their positions. A negative exponent on top can be brought to the bottom so it's a reciprocal, and vice versa. Cease by simplifying.
At that place's frequently more than 1 way to simplify negative exponent expressions. Since exponents are repeated multiplication, and you can multiply numbers in whatever order you lot'd like, unlike steps tin can lead to the same result.
Fractions with negative exponents
We know what to exercise with whole numbers that take negative exponents, but what almost fractions with negative exponents?
To simplify fractions with negative exponents, flip them to their reciprocals, multiply and reduce.

How to teach negative exponents with Prodigy
Students volition love practicing negative exponents with Prodigy: a gratuitous, curriculum-aligned math platform packed with exotic pets, fun challenges and educational adventure.
Negative exponents are an of import concept for students to grasp before they start high school, simply many learners struggle with key concepts. Using powerful reporting tools in yourTeacher Dashboard, you lot'll encounter which topics your students have mastered, and where they need more practise.
Prodigy'due southAssignments, Plans and Test Prep features allow you assign targeted math exercise for students who are struggling or excelling. You'll get real-time data as students play, and you'll be able to deliver differentiated assignments that align with what you're teaching in class. You can use Prodigy to:
- Deliver spiral assessments
- Prepare for standardized tests
- Reinforce in-form lessons (like negative exponents!)
Final thoughts on negative exponents
If you lot'd like more practice on exponents in general, our exponent rules worksheet gives students the opportunity to become more than familiar with how exponents piece of work.
When working with negative exponents, information technology's important to remember all the exponent rules stay the same. As well this, the only matter students need to know is how to add, subtract, multiply and split up negative numbers.
Accept information technology tiresome, and build upwards to more than complicated questions. Your students will be exponent whizzes in no time at all!
Get-go teaching negative exponents with Prodigy today. Prodigy is a no-cost, curriculum-aligned math platform that encourages students to love learning math. With over a million teachers and 50 million students, Prodigy offers unique solutions for your classroom.

Source: https://www.prodigygame.com/main-en/blog/negative-exponents/
0 Response to "what does a base raised to a negative exponent mean"
ارسال یک نظر